▣ 문제
세종대왕은 현수에게 현수가 다스릴 수 있는 영지를 하사하기로 했다. 전체 땅은 사각형으로 표 시된다. 그 사각형의 땅 중에서 세종대왕이 현수가 다스릴 수 있는 땅의 크기(세로의 길이와 가 로의 길이)를 정해주면 전체 땅 중에서 그 크기의 땅의 위치를 현수가 정하면 되는 것이다. 전체 땅은 사각형의 모양의 격자로 되어 있으며, 그 사각형 땅 안에는 많은 오렌지 나무가 심겨져 있다. 현수는 오렌지를 무척 좋아하여 오렌지 나무가 가장 많이 포함되는 지역을 선택하고 싶어 한다. 현수가 얻을 수 있는 영지의 오렌지 나무 최대 개수를 출력하는 프로그램을 작성하세요. 다음과 같은 땅의 정보가 주어지고, 현수가 하사받을 크기가, 가로 2, 세로 3의 크기이면 가장 많은 오렌지 나무가 있는 영지는 총 오렌지 나무의 개수가 16인 3행 4열부터 시작하는 구역이다.
▣ 입력설명
- 첫 줄에 H(세로길이)와 W(가로길이)가 입력된다. (1<=H, W<=700) 그 다음 H줄에 걸쳐 각 사 각형 지역에 오렌지의 나무 개수(1~9개) 정보가 주어진다. 그 다음 영지의 크기인 세로길이(1~H)와 가로길이(1~W)가 차례로 입력된다.
▣ 출력설명
- 첫 줄에 현수가 얻을 수 있는 오렌지 나무의 최대 개수를 출력한다.
▣ 출력설명
| 6 7 3 5 1 3 1 3 2 1 2 1 3 1 1 2 1 3 1 5 1 3 4 5 1 1 3 1 3 2 3 1 1 3 1 1 2 1 3 1 3 1 2 2 2 3 |
▣ 출력설명
| 16 |
-내 코드
#include<stdio.h>
#include<stdlib.h>
int main() {
int H, W, h, w;
int i, j, k, l;
int total;
int max = 0;
scanf("%d %d", &H, &W);
int **map = (int**)malloc(sizeof(int*) * H);
for (i = 0; i < H; i++) {
map[i] = (int*)malloc(sizeof(int) * W);
}
for (i = 0; i < H; i++) {
for (j = 0; j < W; j++) {
scanf("%d", &map[i][j]);
}
}
scanf("%d %d", &h, &w);
for (i = 0; i < H; i++) {
for (j = 0; j < W; j++) {
//시작점이 (i,j)
total = 0;
for (k = 0; k < h; k++) {
for (l = 0; l < w; l++) {
if(i+k < H && j+l < W) total += map[i + k][j + l];
}
}
if (total > max) max = total;
}
}
printf("%d", max);
return 0;
}
이렇게 작성된 코드는 H와 W값이 커지면 제한시간안에 돌지 못한다.
따라서 다르게 접근을 해야된다.
-수정 코드
#include<stdio.h>
#include<stdlib.h>
int map[701][701];
int dp[701][701] = { 0 }; //해당 행, 열까지 모든 원소들의 합
int main() {
int H, W, h, w;
int i, j;
int total;
int max = 0;
scanf("%d %d", &H, &W);
for (i = 0; i < H; i++) {
for (j = 0; j < W; j++) {
scanf("%d", &map[i][j]);
}
}
scanf("%d %d", &h, &w);
for (i = 1; i <= H; i++) {
for (j = 1; j <= W; j++) {
dp[i][j] = map[i][j] + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
}
}
for (i = h; i <= H; i++) {
total = 0;
for (j = w; j <= W; j++) {
total = dp[i][j] - dp[i - h][j] - dp[i][j - w] + dp[i - h][j - w];
if (total > max) max = total;
}
}
printf("%d", max);
return 0;
}
여기서 dp는 해당 행, 열까지 모든 원소들의 합이다.
입력받은 map이 다음과 같다고 하자.
| 3 | 5 | 1 | 3 | 1 | 3 | 2 |
| 1 | 2 | 1 | 3 | 1 | 1 | 2 |
| 1 | 3 | 1 | 5 | 1 | 3 | 4 |
| 5 | 1 | 1 | 3 | 1 | 3 | 2 |
| 3 | 1 | 1 | 3 | 1 | 1 | 2 |
| 1 | 3 | 1 | 3 | 1 | 2 | 2 |
dp[1][1] = 3
dp[1][2] = 3 + 5
dp[2][1] = 3 + 1
dp[2][2] = 3 + 5 + 1 + 2
dp[2][2]를 다른 방법으로 표현하면,
dp[2][2] = (3+5) + (3+1) + (2) - (3)
= dp[1][2] + dp[2][1] + map[2][2] - dp[1][1]
즉, 다음과 같은 식으로 표현이 가능하다.
dp[i][j] = dp[i-1][j] + dp[i][j-1] + map[i][j] - dp[i-1][j-1]
dp로부터 2차원 배열 구간합을 구할 수 있다.
| 3 | 5 | 1 | 3 | 1 | 3 | 2 |
| 1 | 2 | 1 | 3 | 1 | 1 | 2 |
| 1 | 3 | 1 | 5 | 1 | 3 | 4 |
| 5 | 1 | 1 | 3 | 1 | 3 | 2 |
| 3 | 1 | 1 | 3 | 1 | 1 | 2 |
| 1 | 3 | 1 | 3 | 1 | 2 | 2 |
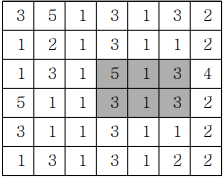
하사 받은 크기가 가로(h)2, 세로(w)3 크기일 때
초록부분의 합은
전체합 - 파란부분합 - 빨간부분합 +겹치는 보라부분합
dp[4][6] - dp[4][3] - dp[2][6] + dp[2][3]
즉, 구간합은 다음과 같이 구할 수 있다.
dp[i][j] - dp[i][j-w] - dp[i-h][j] + dp[i-h][j-w]
이런 식으로 접근을 하면 두 번의 2중 for문으로도 2차원 배열의 구간합을 구할 수 있다.
참고:
영지 선택(2차원 배열 구간합, DP) / c / 제한시간 : 1초
아무거나 내꺼 공부할래 영지 선택(2차원 배열 구간합, DP) / c / 제한시간 : 1초 본문 [c언어] 알고리즘 공부 영지 선택(2차원 배열 구간합, DP) / c / 제한시간 : 1초 mero95 mero95 2021. 1. 29. 18:50 Prev 1 ···
chonstudyroom.tistory.com
'Algorithm' 카테고리의 다른 글
| [백준] 2630번: 색종이 만들기 (재귀) (0) | 2021.02.24 |
|---|---|
| 부분집합(MS 인터뷰, DFS:완전탐색) (0) | 2021.02.05 |
| 이분검색 (0) | 2021.01.29 |
| [개념] 정렬 알고리즘 (0) | 2021.01.25 |
| [개념] 탐색(검색) 알고리즘 (0) | 2021.01.25 |